One-Class Classification Algorithms

In my previous blog entry, I have put forth a case for when the traditional classification algorithms do not perform well i.e. when the training data has reasonable level of imbalance between the various classes. The problem statement that I was trying to solve had a similar problem of the skewed distribution of the training data. The power company had only created the database of fraudulent customers.

As I mentioned in my previous blog post, there are 2 methods to tackle the case when we have data from only one class:

1. The first method is an obvious approach to generate an artificial second class and proceed with traditional classification algorithms.

2. The second one is to modify the existing classification algoriths to learn on the data from only one class. These algorithms are called "one-class classfication algorithms" and include one-class SVM, One-Class K-Means, One-Class K-Nearest Neighbor, and One-Class Gaussian.

In this blog entry, I will elaborate on the second method and explain the mathematics behind the one-class classification algorithms and how it improves over the traditional classification algorithms.

Fundamental difference between Binary and One Class Classification Algorithms

Binary classification algorithms are discriminatory in nature, since they learn to discriminate between classes using all data classes to create a hyperplane(as seen in the fig. below) and use the hyperplane to label a new sample. In case of imbalance between the classes, the discriminatory methods can not be used to their full potential, since by their very nature, they rely on data from all classes to build the hyperplane that separate the various classes.

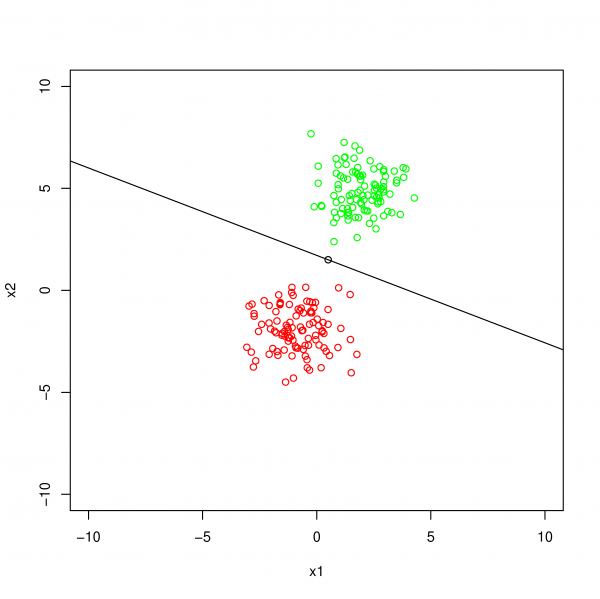Binary Classification Hyperplane

Where as the one-class algorithms are based on recognition since their aim is to recognize data from a particular class, and reject data from all other classes. This is accomplished by creating a boundary that encompasses all the data belonging to the target class within itself, so when a new sample arrives the algorithm only has to check whether it lies within the boundary or outside and accordingly classify the sample as belonging to the target class or the outlier.

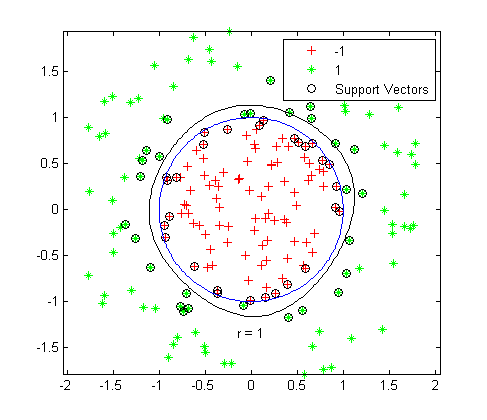One-Class Classification Boundary

Mathematics behind different One-Class Classification Algorithms

In this section, I will explain the mathematics behind different one-class machine learning algorithms by taking a cue from this research paper.

One-Class Gaussian

This is basically a density estimation model. It assumes that the training data are the samples from the Multivariate Normal Population, therefore for a test sample (say z) having n-feaures, the probability of it belonging to the target class can be calculated as follows:

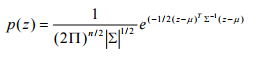
where the parameters μ and Σ are the poputation mean and covariance. Hence, the objective function of this machine learning algorithm is to determine the estimates for μ and Σ. Using the method of maximum likelihood estimator, we can show that the sample mean and sample covariance are the unbiased and consistent estimators for population mean and variance respectively. Hence, once we calculate the probability p(z), we can set a threshold to determine whether a new sample is outlier or not.

One-Class Kmeans

In this method, we first classify the training data into k clusters (which is chosen as per our requirements). Then, for a new sample (say z), the distance d(z) is calculated as the minimum distance of the sample from the centroid of all the k clusters. Now if d(z) is less than a particular thereshold (which is again chosen as per our requirements), then the sample belongs to the target class otherwise it is classified as the outlier.

One-Class K-Nearest Neighbor

Let us take note of some notation before we understand the mathematics behind the algorithm.

d(z,y) : distance between two samples z and y

NN(y) : Nearest Neighbor of sample y

Now given a test sample z, we find the nearest neighbor of z from the training data (which is NN(z) = y) and the nearest neighbor of y (which is NN(y)). Now the rule is to classify z as belonging to the target class when:

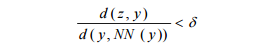
where the default value of δ is 1 but can be chosen to satisfy our requirements.

In my next blog entry, I will try to explain the most widely used one-class classification algorithm i.e. one-class support vector machines. Stay tuned !

Thank you very much for making it this far.