Google Summer of Code 2017

Ayush Pandey

2017-08-26 02:13

Proposal Poster Github

Google Summer of Code 2016 under the Julia Language was an experience of a lifetime which motivated me to apply to this year's program as well. While, my last year project with Convex.jl was hardcore mathematics, this time I wanted to work in the field of Machine Learning (mainly it's application in the field where there was a potential but not much had been explored). I was well aware of the applications of Machine Learning techniques in Computer Vision, Natural Language Processing, Stock Market Predictions but I never heard or read anyone saying that they used Machine Learning in Differential Equations. So, as soon as I read about the project Machine learning tools for classification of qualitative traits of differential equation solutions, I knew what I had to do in the coming summers. It's been awesome 4 months working on my project and I am so thankful to Google Summer of Code 2017 program and The Julia Language for providing me such an incredible opportunity. The thanksgiving note would be incomplete without the mention of my mentor Chris Rackauckas who always helped me whenever I felt like giving up.

In the remaining blog, I will touch upon the technical aspects of my project and my work:

Project Abstract

Differential equation models are widely used in many scientific fields that include engineering, physics and biomedical sciences. The so-called “forward problem” that is the problem of solving differential equations for given parameter values in the differential equation models has been extensively studied by mathematicians, physicists, and engineers. However, the “inverse problem”, the problem of parameter estimation based on the measurements of output variables, has not been well explored using modern optimization and statistical methods. Parameter estimation aims to find the unknown parameters of the model which give the best fit to a set of experimental data. In this way, parameters which cannot be measured directly will be determined in order to ensure the best fit of the model with the experimental results. This will be done by globally minimizing an objective function which measures the quality of the fit. This inverse problem usually considers a cost function to be optimized (such as maximum likelihood). This problem has applications in systems biology, HIV-AIDS study.

The expected outcome of my project was set of a tools for easily classifying parameters using machine learning tooling for users inexperienced with machine learning.

Application - HIV-AIDS Viral Dynamics Study

Studies of HIV dynamics in AIDS research are very important for understanding the pathogenesis of HIV infection and for assessing the potency of antiviral therapies. Ordinary differential equation (ODE) models are proposed to describe the interactions between HIV virus and immune cellular response.

One popular HIV dynamic model can be written as:

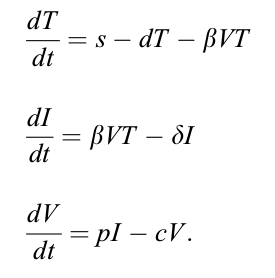
where (T) is target cells which are assumed to be produced at a constant rate s and which are assumed to die at rate d per cell. Productive infection by virus (V), occurs by virus interacting with target cells at a rate proportional to the product of their densities i.e at rate βVT, where β is called the infection rate constant. Productively infected cells (I) are assumed to die at rate δ per cell. Virus is produced from productively infected cells at rate p per cell and is assumed to either infect new cells or be cleared. In the basic model, loss of virus by cell infection is included in the clearance process and virus is assumed to be cleared by all mechanisms at rate c per virion.

Here we assume that the parameters p and c are known and can be obtained from the literature.

Very similar to any Machine Lerning problem, we approached the problem of parameter estimation of differential equations by 2 ways: the Bayesian approach (where the idea is to find the probability distribution of the parameters) and the optimization approach (where we are interested to know the point estimates of the parameters).

Optimization Approach

My mentor Chris had integrated the LossFunctions.jl which builds L2Loss objective function to estimate the parameters of the differential equations. I started by implementing the Two-stage method which is based on based on the local smoothing approach and a pseudo-least squares (PsLS) principle under a framework of measurement error in regression models.

The following is the comparative study of the above two methods:

Advantages

Computational efficiency
The initial values of the state variables of the differential equations are not required
Providing good initial estimates of the unknown parameters for other computationally-intensive methods to further refine the estimates rapidly
Easing of the convergence problem

Disadvantages

This method does not converge to the global/local minima as the Non-Linear regression does if the cost function is convex/concave.

I also wrote implementations and test cases for supporting different optimizers and algorithms such as: 1. Genetic Algorithm from Evolutionary.jl 2. Stochastic Algorithms from BlackBoxOptim.jl 3. Simulated Annealing, Brent method, Golden Section Search, BFGS algorithm from Optim.jl 4. MathProgBase associated solvers such as IPOPT, NLopt, MOSEK, etc.

Then, I integrated the PenaltyFunctions.jl with DiffEqParamEstim to add regularization to the loss function such as Tikhonov and Lasso regularization to surmount ill-posedness and ill-conditioning of the parameter estimation problem.

Bayesian Approach

Our objective was to translate the ODE described in DifferentialEquations.jl using ParameterizedFunctions.jl into the corresponding Stan (a Markov Chain Monte Carlo Bayesian inference engine) code and use Stan.jl to find the probability distribution of the parameters without writing a single line of Stan code.

The exhaustive list of pull requests can be found here.

I am glad to have been successfully implemented what I proposed.